Индуктивность характеризует свойства элементов электрической цепи накапливать энергию магнитного поля. Также это мера связи между током и магнитным полем. Ещё её сравнивают с инерцией электричества – также, как массу с мерой инерции механических тел.
Явление самоиндукции
Если ток, идущий через проводящий контур, изменяется по величине, то возникает явление самоиндукции. В этом случае изменяется магнитный поток через контур, и на выводах рамки с током возникает ЭДС, называемая ЭДС самоиндукции. Эта ЭДС противоположна направлению тока и равна:
ε=-∆Ф/∆t=-L*(∆I/∆t)
Очевидно, что ЭДС самоиндукции равна скорости изменения магнитного потока, вызванного изменением протекающего по контуру тока, а также пропорциональна скорости изменения тока. Коэффициент пропорциональности между ЭДС самоиндукции и скоростью изменения тока называется индуктивностью и обозначается L.
Эта величина всегда положительна, и имеет единицу измерения в СИ 1 Генри (1 Гн). Также используются дробные доли – миллигенри и микрогенри. Об индуктивности в 1 Генри можно говорить, если изменение тока на 1 ампер вызывает ЭДС самоиндукции в 1 Вольт.
Индуктивностью обладает не только контур, но и отдельный проводник, а также катушка, которую можно представить как множество последовательно включенных контуров.
В индуктивности запасается энергия, которую можно вычислить, как W=L*I2/2, где:
- W – энергия, Дж;
- L – индуктивность, Гн;
- I – ток в катушке, А.
И здесь энергия прямо пропорциональна индуктивности катушки.
Важно! В технике индуктивностью также называется устройство, в котором происходит запасание электрического поля. Реальный элемент, наиболее близкий к такому определению – катушка индуктивности.
Общая формула для расчета индуктивности физической катушки имеет сложный вид и для практических вычислений неудобна. Полезно запомнить, что индуктивность пропорциональна количеству витков, диаметру катушки и зависит от геометрической формы.
Также на индуктивность влияет магнитная проницаемость сердечника, на котором расположена обмотка, но не влияет ток, протекающий по виткам. Для вычисления индуктивности каждый раз надо обращаться к приведенным формулам для конкретной конструкции.
Так, для цилиндрической катушки её основная характеристика вычисляется по формуле:
Как правильно выбрать аккумулятор для автомобиля?
L=μ*μ*(N2*S/l),
где:
- μ – относительная магнитная проницаемость сердечника катушки;
- μ – магнитная постоянная, 1,26*10-6 Гн/м;
- N – количество витков;
- S – площадь витка;
- l – геометрическая длина катушки.
Для вычисления индуктивности для цилиндрической катушки и катушек других форм лучше воспользоваться программами-калькуляторами, в том числе онлайн-калькуляторами.
Последовательное и параллельное соединение индуктивностей
Индуктивности можно соединять последовательно или параллельно, получая набор с новыми характеристиками.
Параллельное соединение
При параллельном соединении катушек напряжение на всех элементах равны, а токи (переменные) распределяются обратно пропорционально индуктивностям элементов.
Общая индуктивность цепи определяется, как 1/L=1/L1+1/L2+1/L3. Формула справедлива для любого количества элементов, а для двух катушек упрощается до вида L=L1*L2/(L1+L2). Очевидно, что итоговая индуктивность меньше индуктивности элемента с наименьшим значен
Последовательное соединение
При таком виде соединения через цепь, составленную из катушек, течёт один и тот же ток, а напряжение (переменное!) на каждом компоненте цепи распределяется пропорционально индуктивности каждого элемента:
Суммарная индуктивность равна сумме всех индуктивностей, и будет больше индуктивности элемента с наибольшим значением. Поэтому такое соединение используют при необходимости получить увеличение индуктивности.
Важно! При соединении катушек в последовательную или параллельную батарею формулы расчёта верны только для случаев, когда исключено взаимное влияние магнитных полей элементов друг на друга (экранировкой, большим расстоянием и т.д.). Если влияние существует, то общее значение индуктивности будет зависеть от взаимного расположения катушек.
Некоторые практические вопросы и конструкции катушек индуктивности
На практике применяют различные конструкции катушек индуктивности. В зависимости от назначения и области применения устройства можно выполнить различным способом, но надо учитывать эффекты, возникающие в реальных катушках.
Добротность катушки индуктивности
У реальной катушки, кроме индуктивности, есть ещё несколько параметров, и один из самых важных – добротность. Эта величина определяет потери в катушке и зависит от:
- омических потерь в проводе обмотки (чем больше сопротивление, тем ниже добротность);
- диэлектрических потерь в изоляции провода и каркасе обмотки;
- потерь в экране;
- потерь в сердечнике.
Все эти величины определяют сопротивление потерь, а добротностью называют безразмерную величину, равную Q=ωL/Rпотерь, где:
- ω = 2*π*F – круговая частота;
- L – индуктивность;
- ωL – реактивное сопротивление катушки.
Можно приближённо говорить о том, что добротность равна отношению реактивного (индуктивного) сопротивления к активному. С одной стороны, с ростом частоты растёт числитель, но в то же время за счет скин-эффекта растёт и сопротивление потерь за счет уменьшения полезного сечения провода.
Экранный эффект
Для уменьшения влияния посторонних предметов, а также электрических и магнитных полей и взаимного влияния элементов посредством этих полей, катушки (особенно высокочастотные) часто помещают в экран.
Кроме полезного эффекта, экранирование вызывает снижение добротности катушки, снижение её индуктивности и повышение паразитной ёмкости. Причём чем ближе стенки экрана к виткам катушки, тем выше вредное влияние.
Поэтому экранированные катушки практически всегда выполняют с возможностью подстройки параметров.
Подстроечная индуктивность
В некоторых случаях требуется точно установить значение индуктивности на месте после подключения катушки к другим элементам цепи, компенсируя отклонение параметров при настройке.
Для этого применяются разные способы (переключения отводов витков и т.п.), но наиболее точный и плавный метод – подстройка с помощью сердечника.
Он выполняется в виде стержня с резьбой, который можно вворачивать и выворачивать внутри каркаса, настраивая индуктивность катушки.
Переменная индуктивность (вариометр)
Там, где требуется оперативная регулировка индуктивности или индуктивной связи, применяются катушки другой конструкции. Они содержат две обмотки – подвижную и неподвижную. Общая индуктивность равна сумме индуктивностей двух катушек и взаимной индуктивности между ними.
Изменением относительного положения одной катушки к другой, регулируется общее значение индуктивности.
Такое устройство называется вариометром и часто применяется в связной аппаратуре для настройки резонансных контуров в тех случаях, когда применение конденсаторов переменной ёмкости по каким-то причинам невозможно. Конструкция вариометра довольно громоздкая, что ограничивает область его применения.
Индуктивность в виде печатной спирали
Катушки с небольшой индуктивностью можно выполнять в виде спирали из печатных проводников. Достоинством такой конструкции являются:
- технологичность производства;
- высокая повторяемость параметров.
К недостаткам относят невозможность точной подстройки при регулировке и сложность получения больших значений индуктивности – чем выше индуктивность, тем больше катушка занимает места на плате.
Катушка с секционной намоткой
Индуктивность без ёмкости бывает только на бумаге. При любой физической реализации катушки сразу же возникает паразитная межвитковая ёмкость. Это во многих случаях вредное явление.
Паразитная ёмкость складывается с ёмкостью LC-контура, снижая резонансную частоту и добротность колебательной системы.
Также у катушки возникает собственная резонансная частота, которая провоцирует нежелательные явления.
Для снижения паразитной ёмкости применяют различные способы, самый простой из которых – намотка индуктивности в виде нескольких последовательно включенных секций. При таком включении индуктивности складываются, а суммарная ёмкость снижается.
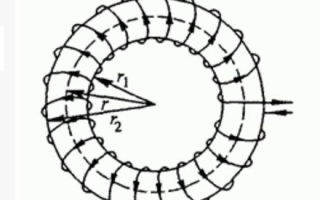
Катушка индуктивности на тороидальном сердечнике
Линии магнитного поля цилиндрической катушки
Линии магнитного поля цилиндрической катушки индуктивности проводят через внутреннюю часть обмотки (если там сердечник – то через него) и замыкаются снаружи через воздух. Этот факт влечёт за собой несколько недостатков:
- снижается индуктивность;
- характеристики катушки меньше поддаются расчёту;
- любой предмет, внесенный во внешнее магнитное поле, меняет параметры катушки (индуктивность, паразитная ёмкость, потери и т.п.), поэтому во многих случаях требуется экранировка.
От этих недостатков во многом свободны катушки, намотанные на тороидальных сердечниках (в виде кольца или «бублика»). Магнитные линии проходят внутри сердечника в виде замкнутых петель.
Это означает, что внешние предметы практически не оказывают влияние на параметры намотанной на таком сердечнике катушки, и экранировка для такой конструкции не нужна.
Также увеличивается индуктивность при прочих равных параметрах, а характеристики проще рассчитать.
Линии магнитного поля тороидальной катушки
К недостаткам катушек, намотанных на торах, относят невозможность плавной подстройки индуктивности на месте. Другая проблема – высокая трудоёмкость и низкая технологичность намотки. Впрочем, это относится ко всем индуктивным элементам в целом, в большей или меньшей степени.
Также общим недостатком физической реализации индуктивности являются высокие массогабаритные показатели, относительно невысокая надежность и низкая ремонтопригодность.
Поэтому в технике от индуктивных компонентов стараются избавляться. Но это возможно далеко не всегда, поэтому намоточные компоненты будут использоваться как в обозримом будущем, так и в среднесрочной перспективе.
Индуктивность
- Номинальная индуктивность:
Заводское значение индуктивности конкретного прибора, измеряется это значение в Генри (производные наноГенри (нГн), микроГенри (мкГн) и т.д). Номинальные значения индуктивностей выбираются из специальных номинальных рядов Е6, Е12, Е24 и т.д.
Допустимое отклонение величины реальной индуктивности от номинальной. Указывается в процентах от номинального значения индуктивности. Допуск может достигать 20%.
Величина тока, при достижении которой, происходит интенсивное рассеяние магнитного потока вне сердечника, что вызывает наведение токов индукции в близко расположенных проводниках.
При периодическом насыщении возникают всплески помех, частоты которых распространяются и на звуковых частотах, и в радиочастотном диапазоне.
Также насыщение сердечника приводит к его перегреву, вплоть до физического разрушения.
- Температурный коэффициент индуктивности:
Параметр, характеризующий зависимость индуктивности катушки от температуры.
Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведёт к изменению собственной ёмкости катушки. Очень существенно влияние температуры на магнитную проницаемость ферромагнетика сердечника.
Маркировка индуктивностей:
Кодовая маркировка:
- Применяется 2 варианта кодовой маркировки:
- 1 Вариант: XYZ обозначает XY•10Z мкГн, причем для индуктивностей менее 10 мкГн десятичным разделителем является буква «R», менее 1 мкГн – буква «N», и в этом случае значение индуктивности в нГн.
- Иначе говоря, первые 2 цифры определяют число (мантиссу), а последняя цифра определяет количество нулей (десятичная степень).
- 2 Вариант: значение номинальной индуктивности непосредственно указано числом в мкГн.
- После цифрового кода указывается буквенный код допуска, в случае его отсутствия – допуск 20%.
Например: 102 — это 10•10² мкГн = 1000 мкГн = 1 мГн, допуск — 20%; 6R8J – 6.8 мкГн, допуск — 5%; R68K – 0.
68 мкГн, допуск — 10%; 22N – 22 нГн, допуск — 20%; 2N2D – 2.2 нГн, допуск — ±0,3 нГн.
Таблица 1 — Кодирование допуска индуктивности.
Цветовая маркировка:
Наиболее часто применяется кодировка 4 или 3 цветными кольцами или точками.
Первые две метки указывают на значение номинальной индуктивности (мантисса) в микрогенри (мкГн, uН), третья метка — множитель (десятичная степень), четвертая — допуск. В случае кодирования 3 метками подразумевается допуск 20%. Цветное кольцо, обозначающее первую цифру номинала, может быть шире, чем все остальные.
Рисунок 2 — Цветовое кодирование индуктивности.
Условное обозначение индуктивностей на схемах:
Рисунок 3 — УГО индуктивности.
- – бескаркасная индуктивность;
- – индуктивность с ферритовым сердечником;
- – индуктивность с сердечником из магнитодиэлектрика, т.е. диэлектрического магнитного материала;
- – индуктивность с ферритовым сердечником с зазором;
- – индуктивность с возможностью регулировки положения ферритового сердечника;
- – переменная индуктивность (вариометр).
Рядом с условным обозначением указывается тип элемента (L) и порядковый номер, также рядом с условным обозначением может указываться (не является обязательным требованием) номинал элемента.
На электрических принципиальных схемах номинальная индуктивность обычно указывается в микрогенри (1 мкГн = 1·103 нГн = 1·10−6 Гн).
Внешний вид катушек индуктивности:
Рисунок 4 — Внешний вид индуктивностей.
Калькулятор индуктивности — перевод единиц индуктивности онлайн
В системе единиц СИ индуктивность измеряется в генри, сокращенно Гн. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. В данном обзоре помимо краткого теоретического обзора представлен калькулятор индуктивности для перевода в десятичные приставки в системе СИ.
Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.
По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током
катушки L=Ψ/i.
Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Поток сцепления катушки индуктивности равен Ψ=L×i.
В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.
- Напряжение на индуктивности уравновешивает ЭДС и может быть записано в
виде uL=-eL=dΨ/dt=L×di/dt. - Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.
- Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
- Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.
Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.
Калькулятор индуктивности онлайн
Калькулятор-конвертер индуктивности позволит быстро перевести Генри в десятичные кратные и дольные единицы.
Множители и приставки СИ для образования десятичных кратных и дольных единиц и их наименований
| Кратные приставки СИ | Дольные приставки СИ |
| Дека-(101). | Деци- (10−1). |
| Гекто- (102). | Санти- (10−2). |
| Кило- (103). | Милли- (10−3). |
| Мега- (106). | Микро- (10−6). |
| Гига- (109). | Нано- (10−9). |
| Тера- (1012). | Пико- (10−12). |
| Пета- (1015). | Фемто- (10−15). |
| Экса- (1018). | Атто- (10−18). |
| Зетта- (1021). | Зепто- (10−21). |
| Иотта- (1024). | Иокто- (10−24). |
Индуктивность | это… Что такое Индуктивность?
Индуктивность микрополосковой линии является распределенной и характеризуется значением индуктивности на единицу длины.
Катушка индуктивности.
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].
В формуле
— магнитный поток, — ток в контуре, — индуктивность.
- Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
.
Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности[4]. Элементами малой индуктивности (применяемыми для больших рабочих частот) могут быть одиночные (в том числе и неполные) витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников[5].
Для имитации индуктивности, т.е. ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются[6] и устройства, не основанные на электромагнитной индукции (см.
Гиратор); такому элементу можно приписать определенную эффективную индуктивность, используемую в расчетах полностью (хотя вообще говоря с определенными ограничивающими условиями) аналогично тому, как используется обычная индуктивность.
Обозначение и единицы измерения
В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт.
В вариантах системы СГС — системе СГСМ и в гауссовой системе индуктивность измеряется в сантиметрах (1 Гн = 109 см; 1 см = 1 нГн)[4]; для сантиметров в качестве единиц индуктивности применяется также название абгенри.
В системе СГСЭ единицу измерения индуктивности либо оставляют безымянной, либо иногда называют статгенри (1 статгенри ≈ 8,987552·1011 генри, коэффициент перевода численно равен 10−9 от квадрата скорости света, выраженной в см/с).
Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz)[8][9]. Единица измерения индуктивности названа в честь Джозефа Генри (Joseph Henry)[10]. Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года[11].
Теоретическое обоснование
- Если в проводящем контуре течёт ток, то ток создаёт магнитное поле[4].
- Будем здесь вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля не настолько сильны и быстры, чтобы ими нельзя было пренебречь в смысле порождения ими магнитного поля.
- Ток считаем одинаковым по всей длине контура (пренебрегая емкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).
По закону Био — Савара величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства пропорциональна этому току.
Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником также пропорционально порождающему току.
Рассуждение выше верно для вакуума.
В случае присутствия магнитной среды[12] (магнетика) с заметной (или даже большой) магнитной восприимчивостью вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме).
Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остается пропорциональным порождающему его току.
Тогда магнитный поток, то есть поток поля вектора магнитной индукции:
через любую конкретную фиксированную поверхность S (в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току B всюду под интегралом.
Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной.
На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближенно рассчитать поток через нее (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже).
Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой).
Итак, мы обосновали:
~
этого достаточно, чтобы утверждать, введя обозначение L для коэффициента пропорциональности, что
В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур.
(Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть ее краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй).
Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.
Но это действительно так: возьмем две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.
Свойства индуктивности
- Индуктивность[13] всегда положительна.
- Индуктивность зависит только от геометрических размеров контура и магнитных свойств среды (сердечника).[14]
Индуктивность одновиткового контура и индуктивность катушки
Величина магнитного потока, пронизывающего одновитковый контур, связана с величиной тока следующим образом[4]:
где — индуктивность витка. В случае катушки, состоящей из N витков предыдущее выражение модифицируется к виду:
где — сумма магнитных потоков через все витки (это так называемый полный поток, называемый в электротехнике потокосцеплением, именно он фигурирует в качестве магнитного потока вообще в случае для катушки в общем определении индуктивности и в теоретическом рассмотрении выше; однако для упрощения и удобства для многовитковых катушек в электротехнике пользуются отдельным понятием и отдельным обозначением), а — уже индуктивность многовитковой катушки. называют потокосцеплением или полным магнитным потоком[15]. Коэффициент пропорциональности иначе называется коэффициентом самоиндукции контура или просто индуктивностью[4].
Если поток, пронизывающий каждый из витков одинаков (что довольно часто можно считать верным для катушки в более или менее хорошем приближении), то .
Соответственно, (суммарный магнитный поток через каждый виток увеличивается в N раз — поскольку его создают теперь N единичных витков, и потокосцепление еще в N раз, так как это поток через N единичных витков).
Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы.
Индуктивность соленоида
Катушка в форме соленоида (конечной длины).
Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки).
При этих условиях и без использования магнитного материала плотность магнитного потока внутри катушки является фактически постоянной и (приближенно) равна
где − магнитная постоянная, − число витков, − ток и − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим[16], что потокосцепление через катушку равно плотности потока , умноженному на площадь поперечного сечения и число витков :
Отсюда следует формула для индуктивности соленоида (без сердечника):
Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель — относительную магнитную проницаемость[17] сердечника:
В случае, когда , можно (следует) под S понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника слишком во много раз.
Более точные формулы для соленоида конечного размера
- Для однослойного (с очень тонкой намоткой) соленоида конечных размеров (не бесконечно длинного) существуют более точные, хотя и более сложные формулы[18]:
- где
— количество витков,
— радиус цилиндра,
— длина его образующей,
,
,
— Эллиптические интегралы.
Это дает
- для
- для
Индуктивность тороидальной катушки (катушки с кольцевым сердечником)
Тороидальная катушка
Для тороидальной катушки, намотанной на сердечнике из материала с большой магнитной проницаемостью, можно приближенно пользоваться формулой для бесконечного прямого соленоида (см. выше):
где — оценка длины соленоида ( — большой радиус тора).
Лучшее приближение дает формула
где предполагается сердечник прямоугольного сечения с наружным радиусом R и внутренним радиусом r, высотой h.
Индуктивность длинного прямого проводника
Для длинного прямого (или квазилинейного) провода кругового сечения индуктивность выражается приближенной формулой[19]:
где − магнитная постоянная, — относительная магнитная проницаемость внешней среды (которой заполнено пространство (для вакуума ), — относительная магнитная проницаемость материала проводника, — длина провода, — радиус его сечения.
Индуктивность единичного круглого витка
Индуктивность витка в форме окружности[19] радиуса R из проводника круглого сечения радиусом r
Определение и формулы для расчета и измерения индуктивности: в чем измеряется
Если существует замкнутый контур, в котором протекает ток, создающий магнитное поле (магнитный поток), то между током и потоком существует взаимосвязь. Коэффициент пропорциональностями между этими величинами является определением индуктивности.
Также эту пропорциональность можно назвать характеристикой инерционности электрической цепи, которая напрямую связана с понятием ЭДС самоиндукции, которая возникает в цепи, когда изменяется сила тока.
Электрическая цепь и индуктивность
Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.
Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.
Самоиндукция и измерение индуктивности
При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.
- Напряжение ЭДС определяется формулой расчета индукции:
- Ꜫ=-L∙di/dt.
- То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».
Обозначение и единицы измерения
От чего зависит индуктивность
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
- В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
- В системе СГСЭ – в статгенри.
Теоретическое обоснование
Ток, протекающий в замкнутом контуре, создает магнитное поле, при этом величина вектора магнитного поля пропорциональна протекающему току. Таким образом, магнитный поток также пропорционален току.
Коэффициент пропорциональности между магнитным потоком и порождающим его током равен индуктивности рассматриваемого контура.
Свойства
Имеет следующие свойства:
- Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
- Не может быть отрицательной;
- Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
- При увеличении частоты тока реактивное сопротивление катушки увеличивается;
- Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.
Схемы соединения катушек
Как радиотехнический элемент, катушки индуктивностей обладают свойствами соединений, полностью идентичными соединениям резисторов.
Параллельное соединение
- Параллельное соединение:
- L=1/(1/L1+1/L2+…+1/Ln).
- Для двух элементов формула упрощается:
- L=L1∙L2/(L1+L2).
Последовательное соединение
Общее значение последовательного соединения равняется сумме индуктивностей:
L=L1+L2+…+Ln.
Добротность катушки
Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.
- Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:
- Q=2∙π∙f∙L/R,
- где:
- π – число пи, ≈3,14,
- f – частота,
- R – сопротивление.
Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает.
Одновитковой контур и катушка
- Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:
- L=Ф/I.
- Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.
- Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:
- L=L1∙N2.
- Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.
Соленоид
Соленоид отличается от обычной катушки по двум признакам:
- Длина обмотки превышает диаметр в несколько раз;
- Толщина обмотки меньше диаметра катушки также в несколько раз.
Соленоидальный тип катушки
- Параметры соленоида можно узнать из такого выражения:
- L=µ0N2S/l,
- где:
- µ0 – магнитная постоянная;
- N – количество витков;
- S – площадь поперечного сечения обмотки;
- l – длина обмотки.
Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника.
Обратите внимание! Используя подвижный сердечник, можно производить оперативное изменение параметров соленоида.
Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.
Тороидальная катушка (катушка с кольцевым сердечником)
- Тороидальный тип обмотки рассчитывается по специальной формуле, которая предполагает, что используется соленоид с бесконечной длиной. Чтобы определять индуктивность формула для тора имеет следующий вид:
- L=µ∙µ0N2S/(2π∙r),
- где r – усредненный радиус тороидального сердечника.
- Кольцевой сердечник прямоугольного сечения можно находить по следующей формуле:
- L=µ∙µ0N2S∙h/(2π)∙ln(R/r),
- где:
- r – внутренний радиус сердечника;
- R – внешний радиус;
- h – высота.
Важно! Вторая формула позволяет узнавать результат с большей точностью.
Длинный прямой проводник
- Как найти индуктивность прямого проводника? Существует формула, дающая точное значение при условии, что проводник имеет длину, значительно превышающую толщину:
- L=µ0/(2π)∙l(µeln(l/r+1/4µi),
- где:
- µe и µi – магнитная проницаемость среды и материала проводника, соответственно;
- l и r – длина и радиус проводника.
Какой магнитной проницаемостью обладает проводник, можно узнать из справочных материалов.
Применение катушек индуктивности
Рассматриваемые элементы широко применяются в радио,- и электротехники:
- Частотозадающие цепи;
- Трансформаторы;
- Дроссели;
- Антенны;
- Элементы фильтров;
- Накопители энергии;
- Нагревательные элементы (система индукционного нагрева);
- Электромагниты;
- Датчики магнитного поля.
Колебательный контур
Емкость и индуктивный элемент, соединенные в цепь, образуют колебательный контур с резко выраженными частотными свойствами и будут являться резонансной системой. В качестве системы используется конденсатор, изменяя емкость которого, можно производить коррекцию частотных свойств.
Последовательный и параллельный колебательные контуры
Если измерить резонансную частоту, используя известный конденсатор, то можно определить индуктивность катушки.
Индуктивность – важнейший элемент в разных областях электротехники. Для правильного применения нужно знать все параметры используемых элементов.
Устройство, которое позволяет определить параметры катушек индуктивности, в том числе добротность, может называться L-метр или Q-метр.
Q-метр для измерения добротности